2 Metaphorical introduction to immanent neural networks
My introduction into the working of a neural network is quite different from that of a mathematician. A mathematician might think that I am missing the essence of it here and there, but as you will see everything works out fine. I am not going to repeat too much of what they have written about it here. I shall write something about it though, in chapter 4, which is about parallel distributed processing, with topics like adjusting neural sensitivity, the generalized delta rule, and error back-propagation.
What a neural network learns how and when
Imagine a neural network to be a school with many neurons in it, most of them being pupils, and some of them being masters. Each master neuron has a group of pupil neurons under him. Each of these, possibly – but probably not – overlapping classes, I call a neural group.
Pupil neurons which are relatively close to each other, can ‘stimulate’ each other. This way, as time goes by, pupils get more and more excited and noisy because of each other. When their master has enough of this, he shouts: “QUIET!” Next, everyone is silent. Then the process starts again, either because of the inherent noisiness of students, or because they are excited from outside their own neural group, the outside being other neural groups, or the world as perceived through the windows of their classrooms.
Summarizing, the pupil neurons continuously tend to activate each other until too many are activated and the master neuron silences them all. The master neurons are otherwise completely ignorant. They don’t teach anybody anything specific.
I must say that actually this picture is a bit wrong. It generally isn’t good for a neural network to produce something of its own without outside stimulation. Such networks tend to go, let’s say, insane. Further more pupil neurons are not connected at random. But I’ll leave such details for later.
Next to teasing others, and getting teased themselves, neurons can do but one thing: remember how often they have been teased successfully by a specific neighbor – for the moment I assume that ‘teasing’ is ‘successful’ if two interconnected pupil neurons are active at the same time.
This remembering means no more than that they’ll be teased by these neighbors more easily in the future every time that these neighbors are activated themselves. In mathematical terms one says that the connection between one neuron and another gains “more weight” when both are activated simultaneously. By this is meant that the inter-neural connection puts more weight in the (partly or wholly unstable) balance of excitation of the neuron. With regard to the metaphor at hand we might say that pupil neurons are getting bruised by each other. At these bruises they become more sensitive than other neurons.
In living brain tissue a connection between two neurons consists of a synapse of one neuron attaching to a dendrite of another. The connection itself is sometimes called a synapse too, which can be confusing. A neuron becomes more sensitive to certain other neurons by chemical and morphological chances in the synaptic connections with these neurons.
It must be said though, that it is not very likely, or at least very uncertain, that in our brains neurons of the same type have direct connections with each other. Thereby human neurons are rather slow. So, in a sense, there won’t be many neurons involved in most neural ‘decision making,’ that is to say, there are many neurons involved, but most of them will, in the end, at a certain moment, not have had much influence. Further more, activation within a neuron is most likely non-linear, which turns the neuron itself in a kind of mini neural network. This can be very advantageous.
In another chapter I shall make a more accurate design, but for educational purposes I’ll stick to this one for a while.
Excitation, activation, depression, inhibition
The teasing of pupil neurons is usually called “excitation.” When a pupil neuron succeeds in activating a certain other neuron one speaks of ’‘activation’.’ Only the simultaneous activation of two interconnected neurons is remembered in the interconnection of one or both of these neurons. Not all neurons necessarily behave like this. Another possibility is that a synaptic connection only gets stronger when the target neuron was already activated.
The ‘’silencing” by the master neuron is usually called “inhibition,” but I like to make a distinction between inhibition and depression, in analogy with ‘activation’ and ‘excitation.’ ‘Depression’ means ‘silencing,’ and only when this succeeds I will speak of ‘inhibition.’
Non-linear activation
The teasing of pupil neurons, with regard to them being teased, cannot be a linear function. If it would be a linear function, that is, if neurons would get activated the same little bit more with every bit that they are teased themselves, then there would be no use for most of the neurons since they in effect all become one.
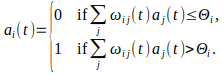
The activation function should be non-linear. For mathematical reasons mathematicians often use a sigmoid function. The simplest formula is a threshold function – which in electronics is called a “trigger” function. A neuron with a threshold activation function turns on when the total of its input signals rises above a certain level. Otherwise it is off – and there’s nothing in between. A binary threshold function can be mathematically expressed as
Here
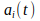
and
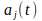
are the activation values of neuron
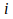
and neuron
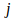
at time
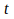
,
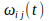
is the weight, strength, or sensitivity of the connection between neuron
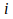
and neuron
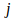
at moment
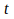
, and
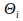
is the threshold level of neuron
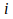
.
More common, quasi-, or semi-linear, differentiable activation functions in artificial neural networks look like this:
Memory traces
Master neurons are always being terribly unfair. As a result of their ‘good intentions’ the pupil neurons which are being teased most often, will be teased even more in the future. Ones a connection of a certain neuron to a certain other neuron becomes more sensitive, this sensitivity tends to grow stronger and stronger. Since the master neuron waits until a certain number of pupil neurons is activated, the result is something like a “memory trace” – this metaphor may be misleading by disguising much of the complexity of neural networks but it is well known. Remember, this memory trace arises while the teacher doesn’t teach anything at all – there is no homunculus. A master neuron selects without intention, nor knowledge.
Some pupil neurons will be activated more, and more often, than others. This would, in the machine built thus far, not have been so if there had not been a master neuron. Without a master neuron, the excitation would have gone on and on. In the end each neuron would have been activated to the fullest – this argument is a bit misleading, because for this not to happen master neurons are not sufficient nor necessary, but I’ll come back to that further on.
You mustn’t think that neurons which are activated more strongly and more often than others are necessarily more sensitive too, nor is it necessary so that their connections are on average more sensitive than those of other neurons. It is not the average sensitivity of a neuron which is important. What’s important is the specific sensitivity of its connections with other neurons.
To give you an image of what is happening inside the kind of neural network which I am making, think of the more sensitive connections between neurons as canals with dikes on each side which lead the flow of neural activation through to a relatively small number of neurons. One might conceive of these as memory traces. I must warn you though, that the word ‘trace’ is misleading since it is always a complex, and usually a completely incomprehensible cluster of traces, which in time leads to the greater activation of certain neurons, and the lesser activation of others. Also this image, which I give here, is completely wrong for the understanding of neural networks which do not have any master-neuron-like mechanism at all. The important point here is to understand the selective, what I call ‘immanizing,’ effects of the activities of a master neuron.
When Sigmund Freud spoke about about the arising of the Ego and the Superego out of the Id, he too used the metaphor of the Dutch landscape with all its dikes along its canals.
From memory traces to activation patterns
For a network as a whole to have any memory which is sensible to us, it needs to be able to associate or remember patterns of activation that where put on its inputs at an earlier time. It should at least be able to recreate such a pattern within itself by re-activating from memory all the neurons that were part of it at an earlier time. This process is called association or auto-association.
Above I vaguely explained how a pattern of neural activation leads to something which we may conceive of as a memory trace. How do we get the activation pattern back, starting from the memory trace? For now I will remain quite vague. It is not so that the same dikes that form the memory trace, lead the activation flow the other way, toward an activation pattern too, but let us for educational purposes conceive of it to work this way nevertheless.
This itself is not too difficult to accept. It gets more complicated when we realize that a neural network can reproduce more than one pattern. Each pattern uses the same dikes and activation canals, but each pattern uses them in a slightly different way, and that makes all the difference. How this is possible, that’s the emphasis of any ordinary mathematical introduction into the working of neural networks. I seem to start at the other end.
Transcendent and immanent neurons
In practice I call neurons, which are activated more often, more “immanent.” Other, less often activated neurons, I call more “transcendent.” These two words will be among the most important of this book. Further on I shall present more refined mechanisms for making neural networks immanent.
In due time my type of network – not all neural networks behave like this! – becomes more and more, what I call, "immanized" or "immanent". This is crucial for the coming into being of that which we experience as the meaning of something, and our consciousness of it.
This does not mean that transcendent neurons have no function. To the contrary. If you imagine yourself a network of neurons with threshold activation functions, this might be a bit difficult to understand, since then the transcendent neurons will be silent most of the time. You’d better take a more fluent, non-linear function, which allows neurons to be more or less active in stead of either ‘on’ or ‘off.’ To give you an image – this is just a metaphor!
[^] – of the function of a transcendent neuron you might think that a transcendent neuron gets activated every time something which is being perceived by the neural network might be this or that. Together the transcendent neurons give all the possibilities. From these possibilities the immanent neurons estimate what it is that the neural network perceives. Without all the work done in advance by transcendent neurons, the immanent neurons could impossibly decide on this.
The terms ‘transcendent’ and ‘immanent’ are relative terms with regard to each other. By this I mean that a certain neuron is more transcendent or more immanent with regard to a certain other neuron. Further on you will see that I shall call the neurons which encode different possibilities immanent too, because in that context they are immanent with regard to other, more transcendent neurons. As such there is a certain hierarchy of immanence. Just compare this with ‘big’ and ‘small.’ An eleven year old child may call itself big at school but small at a wedding. Thereby ‘transcendent’ and ‘immanent’ can be attributed to many things, just like ‘big’ and ‘small.’
Self-desensitizing, and inhibitory neurons
Where does the sensitivity of immanent neurons end? In the current design the immanent neurons would go on becoming more sensitive for ever – even with a master neuron. This would make the imbalance of the network too big. To prevent this from happening one needs some kind of desensitizing mechanism. An easy way to achieve desensitization is by synaptic weight distribution within each neuron. Synaptic weight distribution means that, on average, the sensitivity of each individual neuron is kept the same. If one of its connections gets more sensitive, all the other connections lose a bit, whereby the total remains the same.
In fact neural networks with such ‘self-desensitizing’ neurons can do very well without master neurons, provided that each neuron can both excite and depress other neurons, as is usual in current mathematical models – but unusual in nature.
In mathematical models master neurons are called inhibitory neurons. Inhibitory neurons are, for instance, used to create neural networks which can perform automatic regularity or feature detection. Inhibitory neurons are also used for automatic self-organization, such as with self-organizing maps as invented by Steven Grossberg, and also by Teuvo Kohonen.
For feature detection one typically builds a multi-layer neural network, with input at the bottom, and with as the top-level a so-called winner-take-all, or competitive neural network. This in fact is a layer with only master neurons, and they each try to inhibit each other; so this is different from master neurons silencing pupil neurons. If well-build such a network can, by itself, that is without being thought, learn itself to distinguish features, that is regularities, from its input. In principle it can distinguish as much features as it has master-like, inhibitory neurons. I shall use the same mechanism in chapter 4 to build what I call an “attention mechanism.”
I want my neural network to be able to do both pattern completion, that is auto-association, and feature detection.
One might say that my master neurons are part of a kind of prestructuring of the neural network. Although the master neuron may at this moment, from a mathematical perspective, not seem to be the most essential part of a neural network, it will prove to be of crucial importance in the machinery which I am going to present to you.
Neural activity distribution during sleep?
Many neural networks require a process of de-learning, or un-learning, every now and then. One of the aims is to achieve, what I like to call, “neural activity (re)distribution” over the network as a whole. Without this, large parts of the network might end up being unused, ones memory traces start heading in certain directions. This would create relatively small islands of activity in the network.
[^]It might be that neural activity distribution in a neural network is achieved with the aid of certain sleep periods. If so, then during certain sleep states the sensitization rules of neurons are turned upside down. Instead of connections between two neurons becoming more sensitive when both of them are activated at the same time, they become a little less sensitive. Mind you, the neurons themselves are not asleep, it is the network as a whole which enters a state of sleep. The consequence is that the most active neurons will, during sleep, lose most of their wild feathers.
As I said before, it generally is not good for a network to produce ‘output’ when there is no ‘input’ because that output is usually rubbish. The network should do something with patterns, or information, it perceives. It should not do anything with nothing – that is to say, a perceptual neural network should not do this, but neural networks that have planning and motor functions should, while learning to behave themselves from the reactions which their actions produce in their environment.
Pattern completion and regularity detection
I already gave a small example of what a neural network can do. I took a neural network, attached it to a camera and a monitor, and said that it would try to show that which is in front of the camera onto the monitor by comparing these two images and then adjusting itself. How does this work exactly?
Comparing oneself with something else belongs to the fundamental working principles of a neuron. I refer to the fact that a neuron only gets more sensitive, with regard to a certain other neuron, if both of them are activated. There is an act of comparing involved here.
With regard to the example of apples and pears given earlier, I was not yet referring to any intelligent behavior, but to auto-association. In this each output neuron is connected to its corresponding input, or an input neuron, by way of witch the output can learn to mimic the input. In a very simple neural network the output neuron might even be the input neuron itself. As such the network can learn to associate something with itself.
If a neuron would only be activated by the light which falls on the camera, whereby it shows this on the monitor, than the neural network would have no function. But with a neural network, if you take away part of a known pattern of light which falls on the camera – for example, if you eat from an apple, and show the apple to a neural network which knows apples – then all the neurons belonging to this known pattern will still get activated. As a result the apple will be shown without a bite.
A piece of the pattern may be missing, but the connections between the neurons, which together have learned to form the pattern, have become exactly so much more sensitive and insensitive towards each other, that they make the patterns which they know best from the slightest hint.
In other words, for all these neurons the light which falls on the camera is just one of the many signals they receive. If enough of the rest of their input, coming from other neurons, ‘say’ to go “on,” or “off,” then they will go “on,” or “off,” even without this signal from the camera.
One might conceive of this as a kind of hallucination. The trick of the neural network in our own head is, of course, not to hallucinate. If you do, you go mad. An ordinary neural network would go kind of mad too if it would hallucinate without any perceptual stimulation. It is an important and tricky balance.
In stead of taking away a piece of the pattern of light, one can also take away a piece of the neural network itself. It will still work and it would still contain part or all of its memory! It is even self-repairing, for instance if you put new neurons in. The old neurons will automatically teach the new ones how to behave.
Learning bit by bit
The whole trick of learning for a neural network is to learn a new pattern without distorting old ones. This is what Steven Grossberg calls the problem of massive unlearning, and this is a problem which his neural network does not have.
[^]An ordinary ‘back-prop’ neural network basically learns new patterns by learning all patterns bit by bit, one after the other, repeated many times. Such neural networks cannot remember anything instantly. You have to show the patterns that you want them to learn a hundred times or more, and preferably in random order. This allows them to adjust all patterns with regard to each other by trial and error. This works by each neuron automatically adjusting itself each time that it succeeds or fails. Such an adjustment might lead to another fault, but in the end the network will find the most ideal solution.
Steven Grossberg’s ART neural network does not have this problem. I’ll come back to this in chapter 4.
One pattern at a time in distributed representations
You will have noticed that my neural network, as designed thus far, can handle only one pattern at a time. The activation of this single pattern is spread out over the whole network. Therefore connectionists speak of “distributed representation.”
One can distinguish a special type of representation which I did not mention yet, but which is worth mentioning. It is called “symbolic” or “local representation.” With symbolic representation every neuron stands for a certain thing, usually defined by the makers of the network. The makers say, for example, that this neuron stands for ‘books,’ and that neuron stands for ‘text.’ Next one can teach the network an association between these two. The associations between such neurons can be rather ‘individual,’ or at least they seem to be so from the outside – in fact they are just as distributed, of course.
Symbolic representation has a cognitivist-like representational scheme, but, other than the fundamentally solipsistic, cognitivist models, these neural machines can learn the associations themselves.
The network which I am going to design will have both symbolic and distributed representation. This has a lot to do with the inhibiting master neurons. Therefore their profound introduction.
In a totally non-localized, that is a totally transcendent, distributed network no neuron stands for anything in particular, even though there are, for each thing which it can
recognize, distinct, distributed, activation patterns – ‘recognize’ in the sense of the network being able to complete it.
[^]As opposed to such completely transcendent neural networks I introduce in my system the coming into existence of immanent neurons. Prototypical examples of these have been called “grant-mother-cells.” The term “immanent” is to be taken much more abstractly, tough.
Regarding vision, neural processing starts in our eyes, where neurons accentuate contrasts in light and color. In the visual cortex this is analyzed and the image is, among others, represented as consisting of lines with certain angles, and certain directions of movement, in the form of neurons being activated when a line with a certain angle is present at a certain position in the image. In a following neural layer this is represented in the form of more complex forms, in the sense that certain neurons get activated when certain forms are present at certain places in the image. Again higher in the hierarchy the positions of all these forms with regard to each other are represented, and also one’s own bodily position and location is taken into account. Again higher things get integrated with other sensory information and things come to be recognized as events. Near the top certain things are recognized as objects, intelligible movements, relations, and so on.